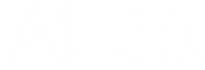Chapter 9: How Do We Locate Disease-Causing Mutations?
(Coursera Week 1)
Yes, the reference human genome is a mosaic of various genomes that does not match the genome of any individual human. Since various human genomes differ by only 0.1%, however, the amalgamation does not cause significant problems.
Huntington's disease is a rare genetic disease in that it is attributable to a single gene, called Huntingtin. This gene includes a trinucleotide repeat "...CAGCAGCAG..." that varies in length. Individuals with fewer than 26 copies of "CAG" in their Huntingtin gene are classified as unaffected by Huntington's disease, whereas individuals with more than 35 copies carry a large risk of the disease, and individuals with more than 40 copies will be afflicted. Moreover, an unaffected person can pass the disease to a child if the normal gene mutates and increases the repeat length. The reason why many repeated copies of "CAG" in Huntingtin leads to disease is that this gene produces a protein with many copies of glutamine ("CAG" codes for glutamine), which increases the decay rate of neurons.
Perhaps in theory, but in practice, biologists still use one reference genome, since comparison against thousands of reference genomes would be time-consuming.
Construct the suffix trie for "papa" and you will see why we have added the "$" sign – without the "$" sign, the suffix "pa" will become a part of the path spelled by the suffix "papa".
If a pattern matches the text starting at position i, we want this pattern to correspond to a path starting at the root of a constructed tree. Therefore, we are interested in the suffix starting at position i rather than the prefix ending at position i.
Although we indeed do not need this edge, it is included to simplify the description of the suffix tree.
The suffix tree for "panamabananas$" reproduced below contains 17 edges with the following labels (note that different edges may have the same labels):
$
a
bananas$
mabananas$
na
mabananas$
nanas$
s$
s$
bananas$
mabananas$
na
mabananas$
nas$
s$
panamabananas$
s$
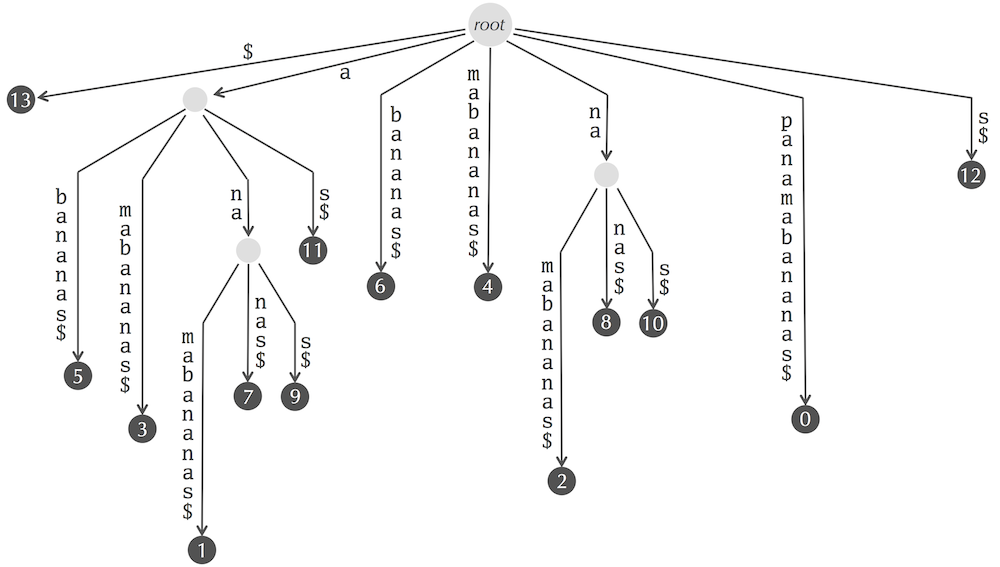
In addition to storing the nodes and edges of the suffix tree, we also need to store the information at the edge labels. Storing this information takes most of the memory allocated for the suffix tree.
Suffix trees were introduced by Weiner, 1973. However, the original linear-time algorithm for building the suffix tree was extremely complex. Although the Weiner algorithm was greatly simplified by Esko Ukkonen in 1995, it is still non-trivial. Check out this excellent StackOverflow post by Johannes Goller if you are interested in seeing a full explanation.
A suffix tree for a string Text has |Text|+1 leaves and up to |Text| other nodes. The last figure in "Charging Station: Constructing a Suffix Tree" illustrates that we need to store two (rather large) numbers for each edge of the suffix tree, each requiring at least 4 bytes for the aprroximately 3 billion nucleotide human genome. Thus, since there are approximately 2·|Text| edges in the suffix tree of Text, the suffix tree for the human genome requires at least 3· 109·2·(4+4) = 48 GB. And we have not even taken into account some other things that need to be stored, such as the human genome itself :)
You can simply construct the suffix tree for the contatenation of all 23 chromosomes. Don't forget to add 22 different delimiters (i.e., any symbols that differ from “A”, “C”, “G”, and “T”) when you construct the concatenated string.
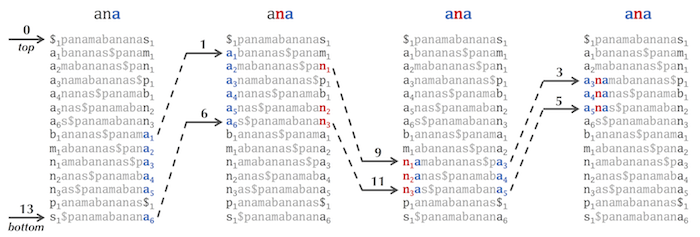
We illustrate how PatternMatchingWithSuffixArray matches "ana" against the suffix array of "panamabananas$", reproduced below from the main text (the suffix array is the column on the left).
- It first initializes minIndex = 0 and maxIndex = |Text| = 13 and computes midIndex = ⌊(0+13)/2⌋ = 6. It then compares Pattern with the suffix "as$" of Text starting at position SuffixArray(6). Since "ana" < "as$", it assigns maxIndex = midIndex - 1 = 5 and computes midIndex = ⌊(0+5)/2⌋ = 2.
- Since "ana" is larger than suffix "amabananas$" of Text starting at position SuffixArray(2), it assigns minIndex - midIndex + 1 = 3 and computes midIndex = ⌊(3+5)/2⌋ = 4.
- Since "ana" is smaller than the suffix "ananas$" of Text starting at position SuffixArray(4), it assigns maxIndex = midIndex - 1 = 3 and computes midIndex = ⌊(3+3)/2⌋ = 3.
- Since "ana" is smaller than the suffix "anamabananas$" of Text starting at position SuffixArray(3), it assigns maxIndex = midIndex - 1 = 2.
The last assignment breaks the first while loop since maxIndex is now smaller than minIndex. As a result, after the first while loop ends, we have maxIndex = 2, minIndex = 3, and
- suffix of Text starting at position SuffixArray(2) = "amabananas$" < "ana"
- suffix of Text starting at position SuffixArray(3) = "anamabananas$" > "ana"
Therefore, the first index of the suffix array corresponding to a suffix beginning with "ana" is first = 3.
The second while loop finds the last index of the suffix array corresponding to a suffix beginning with "ana".
- PatternMatchingWithSuffixArray first sets minIndex = first = 3, maxIndex = |Text| = 13, and computes midIndex = ⌊(minIndex + maxIndex)/2⌋ = ⌊(3+13)/2⌋ = 8.
- Since "ana" does not match the suffix "mabananas$" of Text starting at position SuffixArray(8), it assigns maxIndex = midIndex - 1 = 7 and computes midIndex = ⌊(3+7)/2⌋ = 5.
- Since "ana" matches the suffix "anas$" of Text starting at position SuffixArray(5), it assigns minIndex = midIndex + 1 = 6 and computes midIndex = ⌊(6+7)/2⌋ = 6.
- Since "ana" does not match the suffix "as$" of Text starting at position SuffixArray(6), it assigns maxIndex = midIndex - 1 = 5.
The last assignment breaks the second while loop and assigs last = maxIndex = 5 as the last index of the suffix array corresponding to a suffix beginning with "ana".
To better understand the logic of PatternMatchingWithSuffixArray, you may want to check the FAQ on modifying BinarySearch for determining how many times a key is present in an array with duplicates.
The suffix array for the human genome indeed has about 3 billion elements. However, since each element represents one of 3·109 positions in the human genome, we need 4 bytes to store each element.
It may seem easier to subsequently add each suffix to the growing suffix tree by finding out where each newly added suffix branches from the growing suffix tree. But this straightforward approach results in quadratic running time, compared to the linear time algorithm in the textbook. (Keep in mind that the LCP array can be constructed in linear time.)
(Coursera Week 2)
Our naive approach to constructing BWT(Text) requires constructing the matrix M(Text) of all cyclic rotations, which requires O(|Text|2) time and space. However, there exist algorithms constructing BWT(Text) in linear time and space. One such algorithm first constructs the suffix array of Text in linear time and space, then uses this suffix array to construct BWT(Text).
In short, the last column is the only invertible column of the Burrows-Wheeler matrix. In other words, it is the only column from which we are always able to reconstruct the original string Text.
For example, strings 001 and 100 have identical third columns in the Burrows-Wheeler matrix, as shown below.
$001 $100
001$ 0$10
01$0 00$1
1$00 100$
In practice, it is possible to compute the Last-to-First mapping of a given position of BWT(Text) with very low runtime and memory using the array holding the first occurrence of each symbol in the sorted string. Unfortunately, the analysis is beyond the scope of this class. For details, please see Ferragina and Manzini, 2000 (click here for full text).
We indeed do not use FirstColumn in BWMatching. Although it seemingly does not make sense, we prefer this because we use FirstColumn in a modification of of BWMatching in a later section.
When we use FirstColumn to construct FirstOccurrence, we can immediately release the memory taken by FirstColumn. Furthermore, there is an alternative way to construct FirstOccurrence without using FirstColumn.
Given an index ind in the array LastColumn (varying from 0 to 13 in the example shown in the text), the number of occurrences of symbol before position ind (i.e., in positions with indices less than ind) is defined by Countsymbol(ind, LastColumn). Since the number of occurrences of symbol starting before position ind is equal to Countsymbol(ind, LastColumn), the rank of the first occurrence of symbol starting from position ind is
To be more precise, it is Countsymbol(ind, LastColumn) + 1 if symbol occurs in LastColumn at or after position ind.
Similarly, the rank of the last occurrence of symbol starting before or at position ind is given by
For example, when ind = 5, the rank of the first occurrence of "n" starting at position 5 is Count"n"(5, LastColumn) + 1 = 1 + 1 = 2. On the other hand, the rank of the last occurrence of "p" starting before or at position ind is Count"p"(6, LastColumn) = 1.
Let's match "nam" against BWT("panamabananas$"), but instead of matching backward (like in the figure below, reproduced from the text), let's try to match it forward. We can easily find the three occurrences of "n" in the first column to start this matching, but afterwards we need to match the next symbol "a" in "nam". However, this symbol is "hiding" in the second column, and we have no clue what is in the second column - the Burrows Wheeler Transform does not reveal this information! And there is no equivalent of the "First-Last Property" for the second column to help us.
The condition "top ≤ bottom" is a loop invariant, or a property that holds before and after each iteration of the loop. In this case, if pattern matches have been found, the number of matches is equal to bottom - top + 1. If pattern matches are not found, then at some point in the loop, bottom becomes equal to top - 1, in which case top ≤ bottom and the loop terminates.
No; however, you can easily modify BetterBWMatching by first checking whether Pattern contains symbols not present in Text and immediately returning 0 in this case.
Try "walking backwards" to find the one pattern match of "ban" in "panamabananas$".
(Coursera Week 3)
Selecting a large value of K reduces the memory allocated to the partial suffix array by a factor of K but increases the time needed to "walk backward" during the pattern matching process (see the figure below, reproduced from the main text). This backward walk may take up to K-1 steps ((K-1)/2 steps on average). Thus, it makes sense to select the minimum value of K that allows fitting the BWT pattern matching code into the memory on your machine.

The partial suffix array can indeed be constructed without constructing the (full) suffix array first. The figure below shows the partial suffix array of Text = “panamabananas$” with K = 5. Although it is unclear how to find where the entries 0, 5, and 10 in the suffix array are located without constructing this array first, we know that the top-most entry of the suffix array is 13, corresponding to the length of Text):

Using the LastToFirst function, we can find out where entry 12 is located:

And in turn, we can find entry 11:

At last, we find entry 10, which is the one we were looking for!

After entry 10 in the partial suffix array is found, we can apply the LastToFirst function five more times and find the position of 5 in the partial suffix array. Slowly but surely, after another round of five applications of the LastToFirst function, we will find the position of 0.
However, since the LastToFirst function consumes a lot of memory, we cannot explicitly use it to construct the partial suffix array. We could also use the Count arrays, but these require a lot of memory too… yet we can substitute the Count arrays by memory-efficient checkpoint arrays (which can also be computed without needing the original Count arrays) to achieve the same goal, and therefore construct the partial suffix array efficiently.
We indeed got rid of the LastToFirst array; however, in the same section we saw how the Count arrays can be used as a substitute for LastToFirst.
Selecting a large value of C reduces the memory allocated to the checkpoint arrays by a factor of C but increases the time for computing top and bottom pointers by a factor of C in the worst case. Thus, it makes sense to select the minimum value of C that allows fitting the BWT pattern matching code into the memory on your machine.
To explain how to modify BetterBWMatching for working with checkpoint arrays, we explain how to quickly compute each value in the count array given the checkpoint arrays and LastColumn.
To compute Countsymbol(i, LastColumn), we represent i as t·K + j, where j < K. We can then compute Countsymbol(i, LastColumn) as Countsymbol(t·K, LastColumn) (contained in the checkpoint arrays) plus the number of occurrences of symbol in positions t·K + 1 to i in LastColumn.
Biologists usually set a small threshold for the maximum number of mismatches, since otherwise read mapping becomes too slow.
For example, does Pattern = "TTACTG" match Text = "ACTGCTGCTG" with d = 2 mismatches? Not according to the statement of the Multiple Approximate Pattern Matching Problem, since there is no starting position in Text where Pattern appears as a substring with at most d mismatches. However, if you want to count approximate matches falling off the edges of Text, you can simply add short strings formed by "$" signs before the start and after the end of Text.
Unfortunately, the running time scales roughly as Ak, where A is the alphabet size and k is the number of mismatches. This is why the existing read matching tools based on the Burrows Wheeler Transform become prohibitively slow when the number of mismatches increases. For more details, see N. Zhang, A. Mukherjee, D.Adjeroh, T. Bell. "Approximate Pattern Matching using the Burrows-Wheeler Transform." Data Compression Conference, 2003, 458.
After finding a seed of length k that starts at position i in Pattern and position j in Text, approximate pattern matching algorithms find a substring of Text of length |Pattern| that starts at position j-i. If this substring matches Pattern with at most d mismatches, then it is reported as an approximate match between Pattern and Text.
To find all k-mers that score above a threshold against a given k-mer a, we can generate the 1-neighborhood of a and retain only k-mers from this set that score above the threshold. Iterate by applying the same procedure to each k-mer in the constructed set. See the BLAST paper for a more efficient algorithm.
After finding a seed, BLAST does construct an alignment but imposes a limit on the number of insertions and deletions in this alignment. For example, after finding the two amino acid-long seed CG below, we can find the best local alignment starting at the “end” of this seed (shown by the blue rectangle shown below) and another local alignment ending at the “beginning” of this seed (the corresponding rectangle is not shown). The resulting local alignments extending this seed from both sides form a full-length alignment.
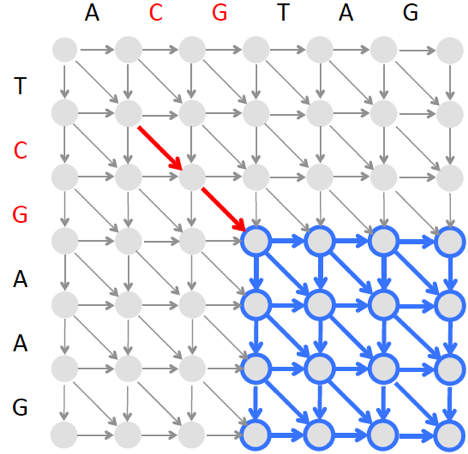
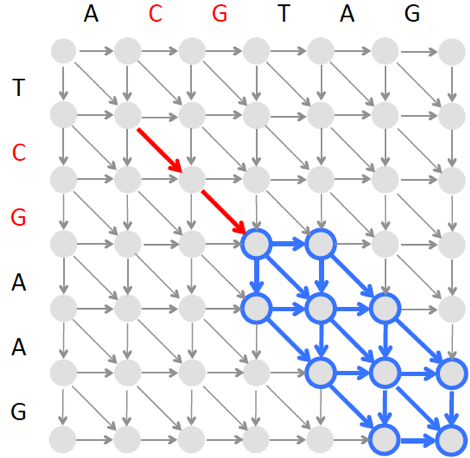
However, since finding an optimal local alignment in the blue rectangle above is time consuming, BLAST instead finds a highest-scoring alignment path in a narrow band as illustrated below. Since the band is narrow, the algorithm constructing this banded alignment is fast.
The algorithm illustrated in the epilogue would fail to find an approximate match of "nad" because the final symbol of "nad" does not appear in "panamabananas$". To address this complication, we can modify the algorithm for finding a pattern of length m with up to k mismatches as follows.
We first run the algorithm described in the main text to find all approximate instances of a Pattern of length k against Text. However, this algorithm does not actually find all approximate matches of Pattern – since we do not allow mismatched strings in the early stages of BetterBWMatching, we miss those matches where the last letter of Pattern does not match Text. To fix this shortcoming, we can simply find all locations in Text where the prefix of Pattern of length k - 1 has d - 1 mismatches. Yet this algorithm fails to find matches where the last two letters of Pattern do not match Text. Thus, we need to run the algorithm again, finding all locations in Text where the prefix of Pattern of length k - 2 has d - 2 mismatches. We then find all locations in Text where the prefix of Pattern of length k - 3 occurs with d - 3 mismatches, and so on, finally finding all locations in Text where the prefix of Pattern of length k - d occurs exactly.
Yes, this strategy would fail to match a read with an error at the first position. However, as noted in the main text, if we start considering mismatches at the first position, the running time will significantly increase. As is, the running time explodes with the increase in the maximum number of errors. If one wants to alow mismatches at the first position, a more sensible strategy would be to trim the first position of the read.
To see how modern read mapping algorithms get around this limitation, see B.Langmead, C. Trapnell, M. Pop, S. L Salzberg. Ultrafast and memory-efficient alignment of short DNA sequences to human genome (2009) Genome biology, 10, R25.
Consider the strings "mapa" and "pepap", with longest shared substring “pa”. If we use both “#” and “$”, then we construct the suffix tree for "mapa#pepap$", which reveals the longest shared substring “pa”. If we do not use “#”, then we construct the suffix tree for "mapapepap$", falsely concatenating the two strings. In this suffix tree, we would find the erroneous longest shared substring “pap” in the concatenated string "mapapepap$".
If key appears in Array[minIndex,…, maxIndex], BinarySearchTop and BinarySearchBottom find the indexes of its first and last occurrences, respectively. Note that in the case of BinarySearchTop, key >Array(i) for all i < minIndex and key ≤ Array(i) for all i>maxIndex. In contrast, in the case of BinarySearchBottom, key ≥ Array(i) for all i<minIndex and key < Array(i) for all i>maxIndex.
BinarySearchTop(Array, key, minIndex, maxIndex)
while maxIndex ≥ minIndex
midIndex = (minIndex + maxIndex)/2
if Array(midIndex) ≥ key
maxIndex = mid-1
else
minIndex = mid+1
return minIndex
BinarySearchBottom(Array, key, minIndex, maxIndex)
while maxIndex ≥ minIndex
midIndex = (minIndex + maxIndex)/2
if Array(midIndex) > key
maxIndex = mid-1
else
minIndex = mid+1
return minIndex