Chapter 8: How Did Yeast Become a Wine-Maker?

To make sense of a gene expression matrix, biologists often rearrange its genes so that similar expression vectors correspond to consecutive rows in the gene expression matrix. Then, they often assign colors to each element of the gene expression matrix according to their expression levels, resulting in a heatmap (shown below).

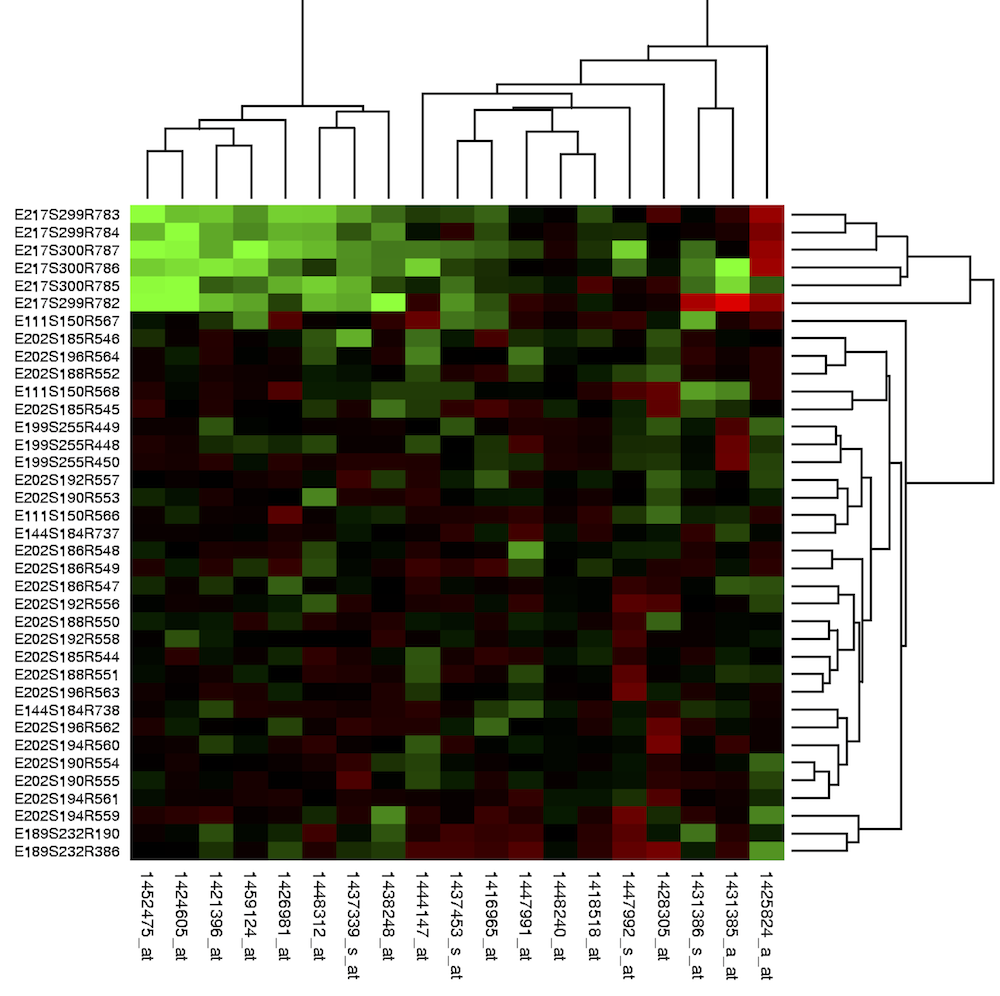
Figure: The heatmap of a gene expression matrix. The rows and columns of the gene expression matrix are ordered according to the order of leaves constructed using hierarchical clustering.

Before clustering even starts, biologists have to decide how to represent expression vectors in multi-dimensional space. Some representations may result in better clustering outcomes than others (see the FAQ on how scaling the input data affects clustering). It turns out that taking logarithms results in better clustering, but there is no good theoretical justification for this observation.

We are interested in all genes that may be implicated in the diauxic shift. If the expression of a gene decreases during the diauxic shift, then chances are it is still relevant to the diauxic shift. For example, the gene may have to be repressed in order to enable the diauxic shift.

The 1-center clustering problem is also known as the Minimum Covering Sphere Problem: given a set of n data points in m-dimensional space, find an m-dimensional sphere of minimum area containing all these points. In the case of two-dimensional space, the corresponding Minimum Covering "Circle" Problem can be solved in O(n⁴) time by considering all triplets of points and capitalizing on the observation that the minimum covering circle for a set of data points is determined by either two points (which represent a diameter of the circle) or three points lying on the boundary of the circle. Thus, we can explore all triples of points. Since checking whether a circle formed by this triple contains all data points takes O(n) time, and we need to check O(n³) triples, the running time of this algorithm is O(n⁴).

There exists a faster linear time algorithm for solving the Minimum Covering Sphere Problem, proposed in N. Megiddo. Linear-time algorithms for linear programming in R³ and related problems. SIAM J. on Computing, 12: 759–776 (1983).

Yes. Simply substitute d(DataPoint, Centers) by Distortion(DataPoint, Centers) in the psesudocode for FarthestFirstTraversal.

The silhouette value is a popular approach for evaluating the quality of clustering. For each point DataPoint, define ClusterDistance(DataPoint) as the average distance between this point and all other points within the same cluster. We also define Distance(DataPoint, Cluster) as the average of the distances from DataPoint to all points in Cluster. The cluster with the minimum distance from a data point (among all clusters that do not contain DataPoint) is called the neighboring cluster for DataPoint. We refer to this distance as NeighborDistance(DataPoint). We define

The silhouette value Silhouette(DataPoint) is defined as follows:

The silhouette value ranges from −1 to +1 and measures how similar a data point is to its own cluster compared to other clusters. A high silhouette value indicates that the data point is well matched to its own cluster and poorly matched to neighboring clusters. If most data points have a high silhouette value, then the clustering is adequate. If many data points have low silhouette values, then the clustering configuration may have too many or too few clusters. The average silhouette value over all data points is a measure of how well the data have been clustered.

To remove outliers, we must first define what we mean by an outlier. It turns out that outlier detection is related to clustering, and so it is not easy to define what an outlier is without clustering! In fact, a common approach to defining outliers is to apply the Lloyd algorithm and list as outliers the top m points that are the farthest away from their nearest cluster centers. However, the Lloyd algorithm itself is sensitive to outliers, and such outliers may have an impact on the clusters that this algorithm constructs. :) Moreover, some outliers may form small tight clusters (e.g., clusters consisting of two data points) that will not be removed by the described procedure. An attempt to remove all small clusters as outliers is also risky, since some small clusters may represent a feature of a dataset rather than an artifact caused by outliers.

Biologists sometimes use the silhouette analysis to select the value of k (see the previous FAQ on alternate metrics of cluster quality). For example, compute the average silhouette values for k ranging from 1 to some max value and find the maximum silhouette value in this range, and select the associated value of k.

The running time of the Lloyd algorithm is proportional to the number of iterations that it requires. Furthermore, each iteration requires O(n*k) distance computations between all data points and all centers, where n is the number of data points and k is the number of centers.

Yes, it may happen that one of the centers has no data points assigned to it, thus reducing the number of clusters.

Given a set of k centers in multi-dimensional space, its Voronoi diagram is a partitioning of the space into k regions (called Voronoi cells), each containing exactly one center. A center's Voronoi cell consists of all points closer to that center than to any other. The figure below (source: https://en.wikipedia.org/wiki/Voronoi_diagram) shows the Voronoi diagram of 20 centers.

For a given center, the Centers to Clusters step of the Lloyd algorithm forms a cluster technically containing all data points in its Voronoi cell. Note that since all points in a cluster are located within a single Voronoi cell, its center of gravity is also located within the same Voronoi cell. Thus, since all Voronoi cells are different, all centers of gravity constructed by the Lloyd algorithm are different. 

k-means++Initializer requires O(n*k) distance computations, where n is the number of data points and k is the number of centers. It therefore results in roughly the same running time as a single iteration of the Lloyd algorithm.

Since FarthestFirstTraversal is a deterministic algorithm, its results are defined by selecting the first center (up to tie resolution). Thus, the number of possible initializations is limited by the number of data points. This may present a limitation if we want to run the Lloyd algorithm many times and select the best solution.

Let {n, k} denote the number of partitions of n points into k clusters. We will establish a recurrence relation to compute {n, k}. To do so, select an arbitrary point x, and note that there are two possibilities. First, x could belong to a cluster all by itself. In this case, the remaining points form k - 1 clusters, and we know that there are {n-1, k-1} ways to partition them. Second, x could belong to a cluster with other points. In this case, there are {n-1, k} ways to partition the other points into k clusters, and then there are k different choices for the cluster to which x belongs.

Combining these two cases results in the following recurrence relation for all n > 1 and all k satisfying 1 < k < n:

As for a base case, note that {n, 1} = 1 for all n ≥ 1 because there is only one way to partition n points into a single cluster. By the same reasoning, {n, n} = 1 for all n ≥ 1.

Exercise Break: Find a formula for {n, 2} in terms of n.

The numbers {n, k} are called Stirling numbers of the second kind.

Given two vectors a = (a₁, …, a_n) and b = (b₁, …, b_n), their dot product is defined as the sum of pairwise products of their elements:

Note that the two occurrences of the "·" symbol in this equation mean different things. On the left side, it represents the dot product of vectors, which we have just defined. On the right side, it indicates a normal product of two numbers a_i and b_i.

Since there is no information for estimating θ_A in this case, you can arbitrarily select θ_A as a random number in the interval from 0 to 1. Similarly, if HiddenVector consists of all ones, you can arbitrarily select θ_A  as a random number in the interval from 0 to 1.

No, not necessarily.

As explained in the sub-section "Where is the computational problem?", our goal is to find variables that maximize the probability of observing the data Pr(Data|HiddenVector, Parameters).

Of course, feel free to implement it! And it will likely improve your results.

As with many parametrized algorithms, you should experiment with various values (and check which ones makes sense) as there is no golden rule for determining the stiffness parameter.

In theory, the EM algorithm continues until Parameters cease to change. In practice, it is often stopped when the difference between respective values of Parameters in the previous iteration and the current iteration of the algorithm becomes small. Alternatively, the EM algorithm can be run for a fixed number of iterations.

Running time is one issue. The Lloyd algorithm requires O(n*k) comparisons, where n is the number of data points and k is the number of centers. In contrast, the hierarchical clustering algorithm requires O(n²) comparisons just to compute the distance matrix.

Also, since the Lloyd algorithm starts with randomly chosen cluster centers, it may yield different clustering results on different runs of the algorithm. Although this lacks consistency, it may have advantages since you can select the best result out of many initializations. With hierarchical clustering, you will obtain the same final tree each time you run the algorithm (up to breaking ties).

Imagine that you want to cluster 1000 people by their height and weight, and suppose that you measure height in centimeters and weight in grams. In this case, one of your authors will be represented by a 2-dimensional point (185,  92137). Since we use the Euclidean distance, which accounts for the height and weight coordinates equally, the weight will dominate the outcome of our clustering algorithm. A better approach would be to represent weight in kilograms, resulting in the point (185, 92) after rounding, but how do we know what the best way is to scale the data?

A simple generalizable scaling method is based on the formula

x’ = (x-min(x))/(max(x)-min(x)).

For example, if the height of people in the sample varies from 160 to 200 centimeters, and the weight varies from 40 to 100 kilograms, then the data point (185,92) is rescaled as ((185-160)/40, (92-40)/60).